Terms
2's completement
overflow
underflow
carryout 进位
Number
bits can represent anything
Float Number
没有小数点,不能表示分数的原因是,内存中只能表示 ,而最小为
引进小数点
- fixed binary point
- float binary point
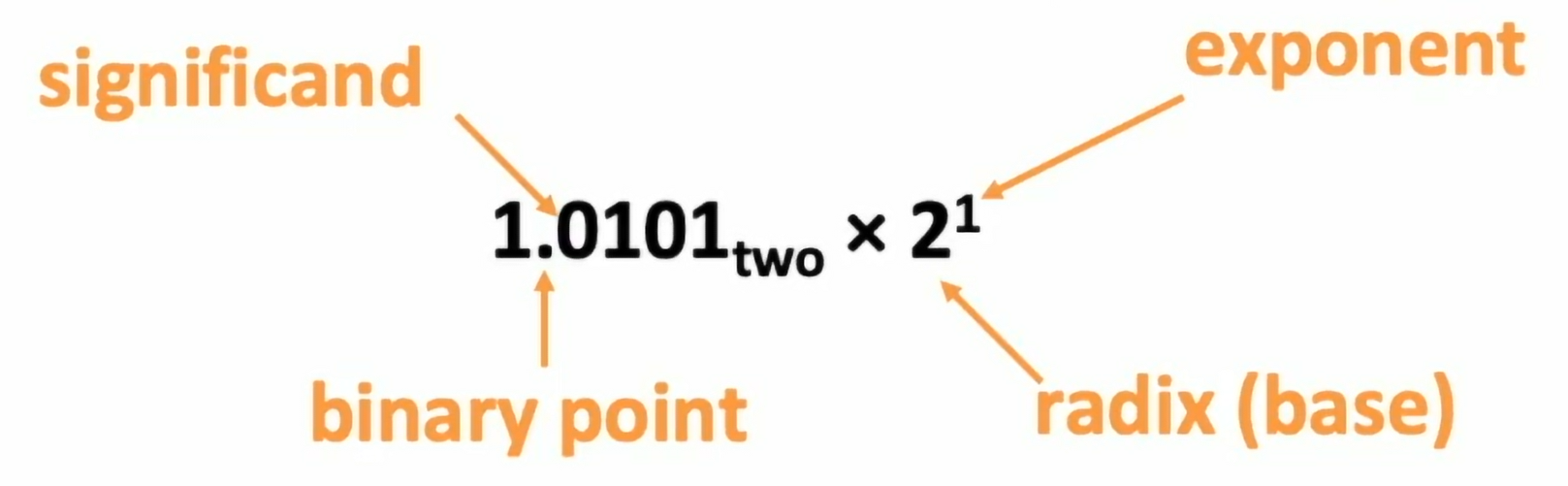
- 使用 normalized scientific notation(binary)
- 最大限度压缩了整数部分(最大长度固定),从而最大程度利用了指数的爆炸性
IEEE 754 标准
分为 sign bit, exponent 和 significand
- Comparison
- 按 S,exponent,significand 优先级比较
- 对 exponent 使用 bais notation(bais -127),因为相比于 Two's Completement,bais notation 可以保持数的线性(顺序性),从而可以更好地比较大小
- 表示 infinity,指数部分全为 1
- float

- double

特殊数表示(!)
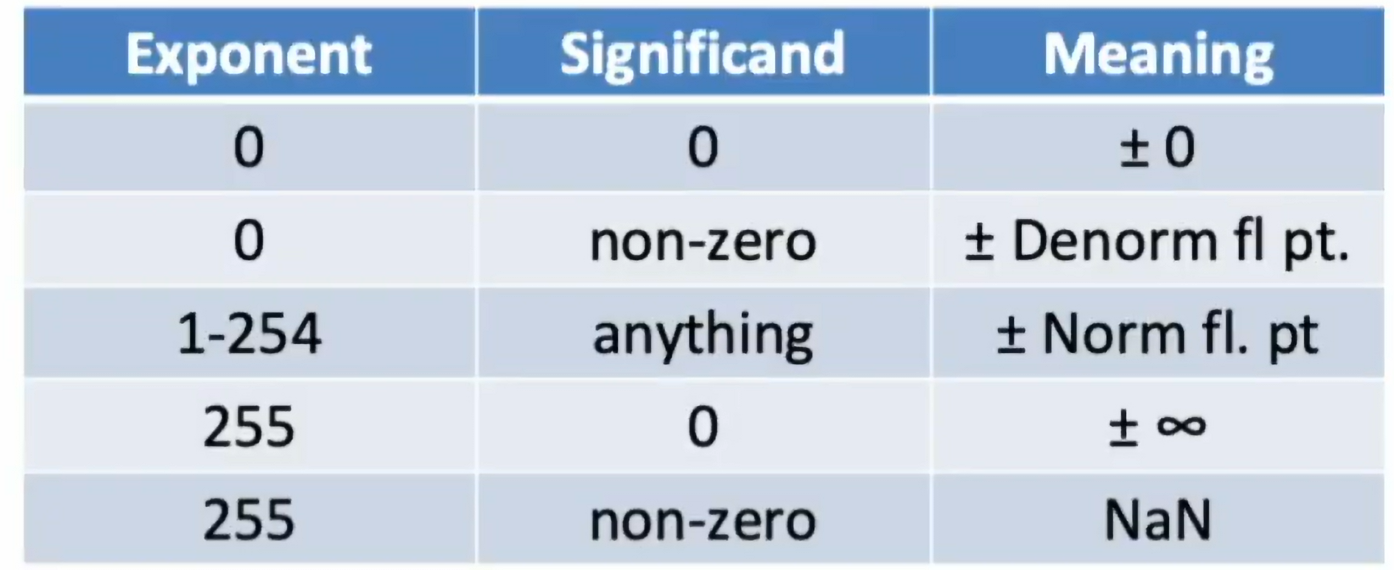
- 当全为 0,表示 0
- 统一了±0
- 当 exponent 全为 1,significand 为 0,表示无穷
- 没有破坏大小顺序
- 当 exponent 全为 1,significand 为非 0,表示 NaN
- 当 exponent 不为 0,表示 norm fl. pt.
- 当 exponent 为 0,significand 为非 0,表示 denorm fl. pt.
- denormalized float number 缩写,即 exponent 部分为 0
- 假设没有所谓 normalize 区分(可以有 ),最小表示 ,但是第二小表示 ,导致 0 和最小数 之间有 gap
- 让先导 1 变成先导 0(让小数点左移 1 位),就可以用 significand 部分表示最小数,则最小数是
significand 位数不是限制,真正的限制是由于先导 1 的这个默认,导致即使 exponent 部分是 0,最小也要乘上指数部分的 ,最小数不够小
对于浮点数,是否意味着可以直接按照 signed number 一样比较?即先比符号位,把后两部分作为整体按照 unsigned number 比较
exponent 和 significand 都具有非负性,有序性;exponent 大这个浮点数一定大;高位有值,意味着这个数也更大
Problems
- overflow & underflow
- n 个 bit 最多表示 个数,所以不可能表示所有实数
- 越接近 0,表示的数越密集(增长速度取决于指数,e.g.: 与 之间差 )
- FP addition 近似
- Big+Little == Big
位数不同的两个数相加减时候,需要对阶(小数点对齐,指数变化),对阶过程永远是小往大对阶,阶小的时候会有有效位丢失
memory
分成 stack, heap, static data, code
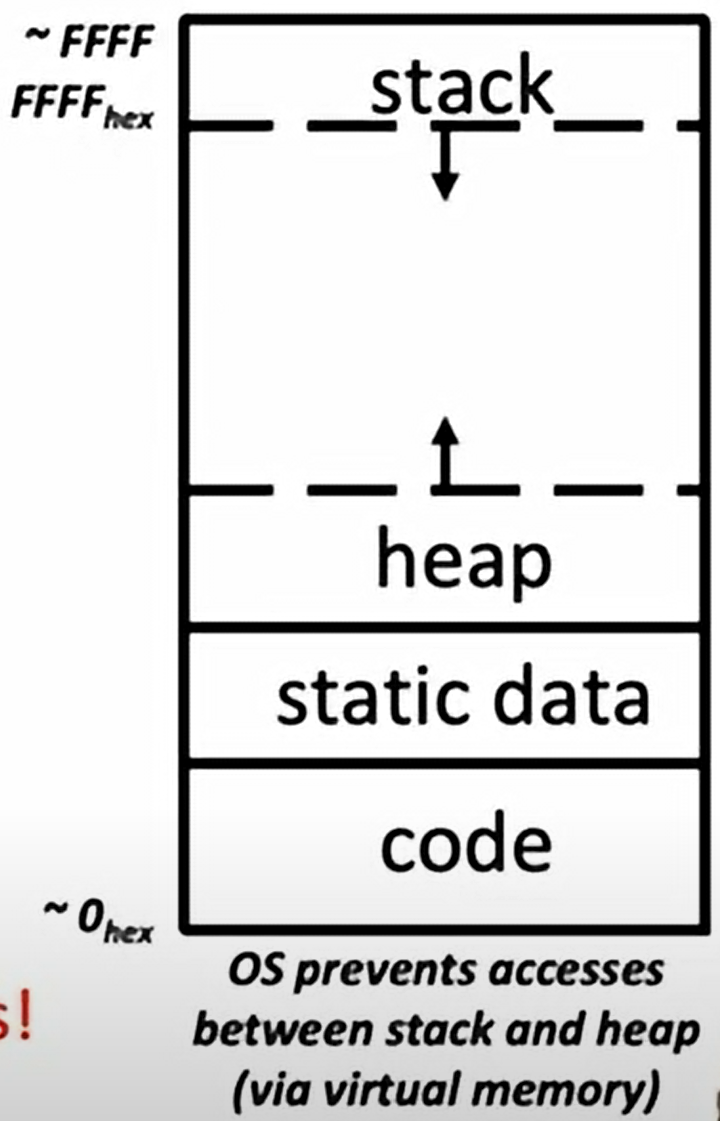
without interfering 几个部分不会相互重叠
stack
一个 stack frame 包括了一个调用函数的整体
argument, variables, caller function location
SP(stack pointer) 指向 lowest(current) funciton frame
Endianness
内存中的字节顺序,Little-Endianness 是倒序的
- 内存中取出到寄存器后,寄存器不存在 Endianness 的说法,Big/Little Endianness 数据在寄存器中存储方式相同
heap
长度不确定的数据,不能存储在栈中(函数结束后就会被释放)
heap 更为灵活和持久
sizeof()
返回 char-sized units 数量,sizeof(char) 永远是 1
三种分配内存函数
malloc calloc relloc
ex: int * p = (int *) malloc(3, sizeof(int);
calloc 相较于 malloc,分配的内存总是会初始化为 0
relloc 能调整已分配的 heap 内存的大小,返回的指针有不确定性(不要再使用老的指针)
阅读内存分配的 code
Common Memory Problems
- 不要返回局部变量的地址,因为函数结束后局部变量被施放,地址无效
- 函数内释放全局变量导致内存泄漏
- 忘记分配数组结束符的内存
Rule of Thumb: alloc 和 free 数量应该相等
debug tools: Valgrind
Assembly Language (Based on 32bits RISC-V )
汇编语言 Assembly Language(a.k.a.: ASM)
不同的 asm: intel, arm, RISC-V
RISC-V Design Principle: Smaller is Faster
使用 32 个寄存器
Register 寄存器
- 固定大小的小内存(通常为 32bit,64bits 等)
- 读写速度快
- zero register(x0, zero) 值永远为 0,写入无效
- 分类
- safe reg: s0-s11
- temporary reg: t0-t6
- zero reg: x0
Memory Hierarchy

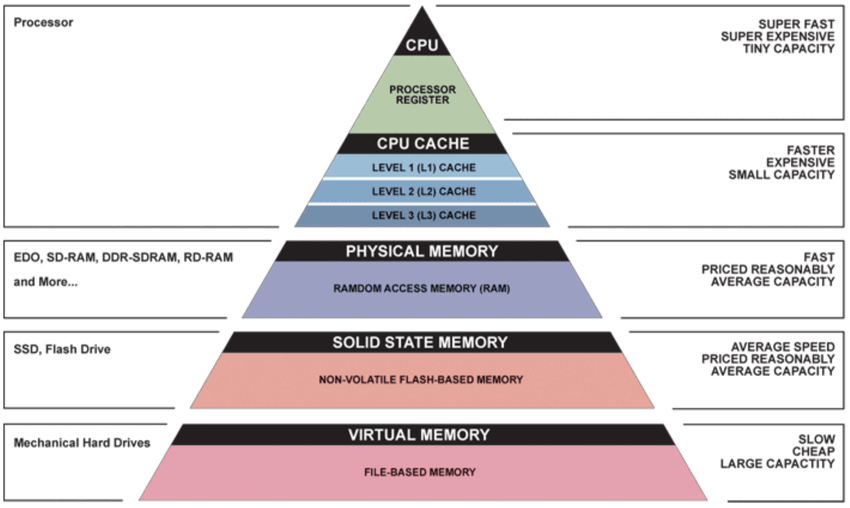
计算机结构
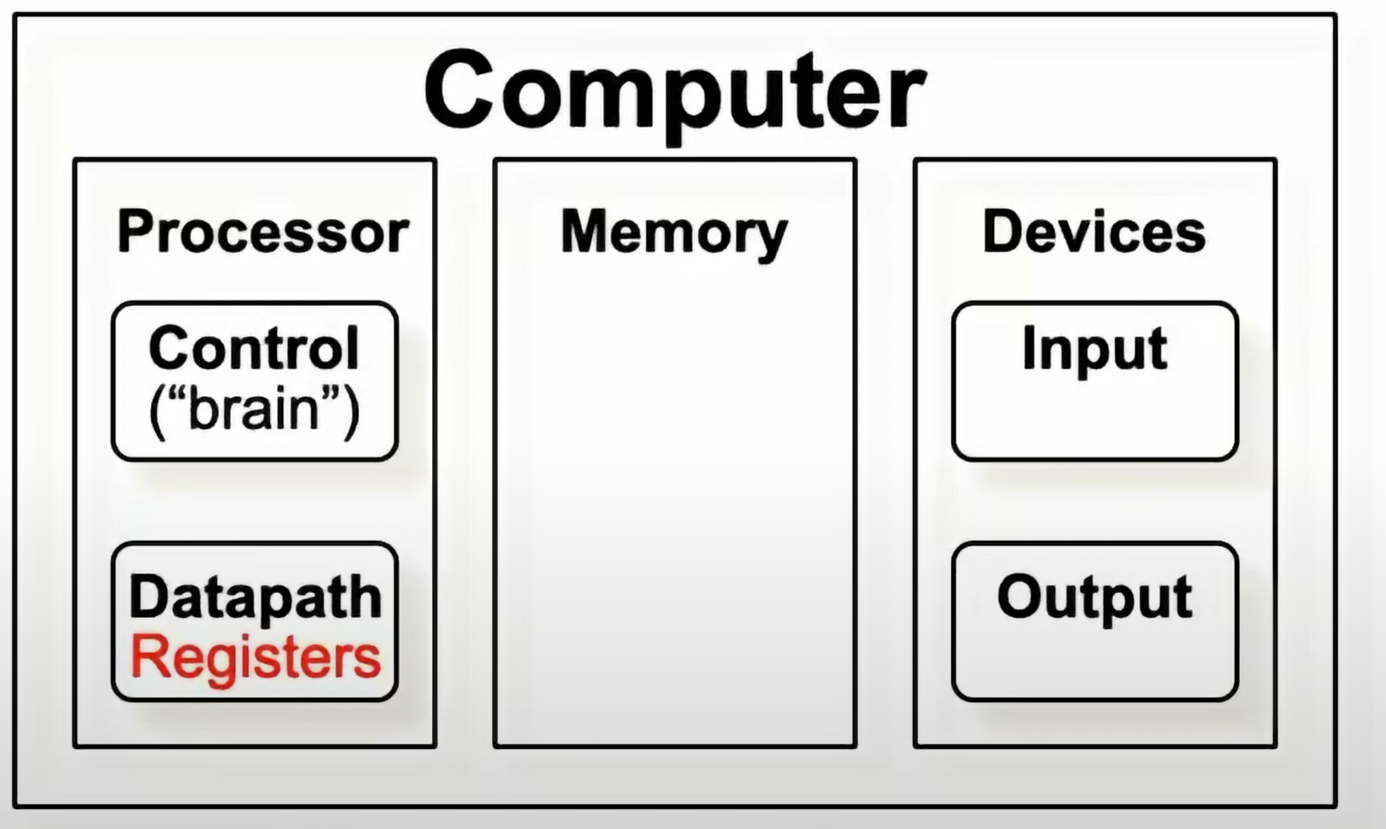
register 是 datapath 的一部分
汇编指令
op dst, src1, src2
immediates
opi dst, src1, imm
Arithmetic Instructions
add addi addw addiw
sub subw
减法可以用加法操作,所以不需要 subi
e.g.: addi s1, s2, 5
Extension Instructions
mul mulhdiv rem
Data Transfer Instructions
memop reg off(bAddr)
对 base address + offset 位置的值进行读写到 reg 中
- RISC-V 的内存是 byte-addressed(按字节寻址) 的,也就是寻找地址的最小单位是字节,offset 单位是 byte
- int 4byte char 1byte
- MB = byte GB = byte TB byte-addressed
- MB 粗略算可以用 1000B 表示
- 1 word = 4 byte = 32 bit,用 8 个 HEX 数/32 个 BIN 数表示,一个 Byte = 2 个 HEX 数 = 8 个 BIN 数
lw sw
branching + data transfer
slt(i)set less than
Branching Instructions
配合 label 使用
op reg1, reg2, label
beq ==
bne !=
blt <
bge >=
j jump
汇编预言中逻辑控制通过 Program Counter(PC) 实现,所有的指令存储在内存得的代码区,label 最终转化成地址,可以被 PC 寻址到
高阶语言中的循环也可以被分解成判断语句 + 操作
Shifting Instructions
逻辑移位和算数移位
- 逻辑移位会 sign-extension
- 算数移位补 0
Bitwise Instructions
and or xor
Environment Call
应用程序与操作系统交互
ecall
Pseudo Instructions
addi dst reg1, 0 -> mv dst, reg1
li la
nop addi x0, x0, 0
Function
调用函数使用 j 指令跳转执行函数体,再通过 ret 指令返回原处。
需要处理变量保存问题,有两类约定:
- 对于 caller-saved/volatile register,caller 有义务在 prolugue 保存在 stack 中,在 epilogue 恢复其值;callee 无需考虑直接使用。包括 t0-t6, a0-a7, ra
- 对于 callee-saved/saved register,caller 无需保存;callee 有义务先保存其值在 stack 中,函数结束前恢复其值。包括 s0-s11 & sp
使用 a register 保存参数和返回值
如果需要保存更多参数,使用 sp 将参数保存在 stack 中
addi sp, sp, -4*#args分配内存
j instructions
j: j labeljal(jump and link): jal dst label- 先 j 再把下一个指令(pc+4 bytes)的地址保存在一个 reg 中
jr(jump register)jalr(jump and link register)- invoke->
jal ra label---- return->jr ra(jump 到 jal 时 link 的 reg) - pseudo instructions
j label==jal x0, labeljr ra==jalr x0, ra, 0==ret
调用函数流程

Instructions Format
(整体层面)
instructions 如何转化成二进制?
- 程序作为内存的一部分被保存,使用 PC 来定位 instruction 语句进行执行
- 每条语句根据汇编语言规定转化为固定长度的二进制(e.g.: RISC-V asm -> 32bits)
(局部层面)
具体如何转化语句?
- 使用不同 format,不同 format 通过 32bits 结尾的 opcode 这个 7 个字节识别区分
- 通过 funct 进一步识别区分,具体为某条 instruction
- format 表
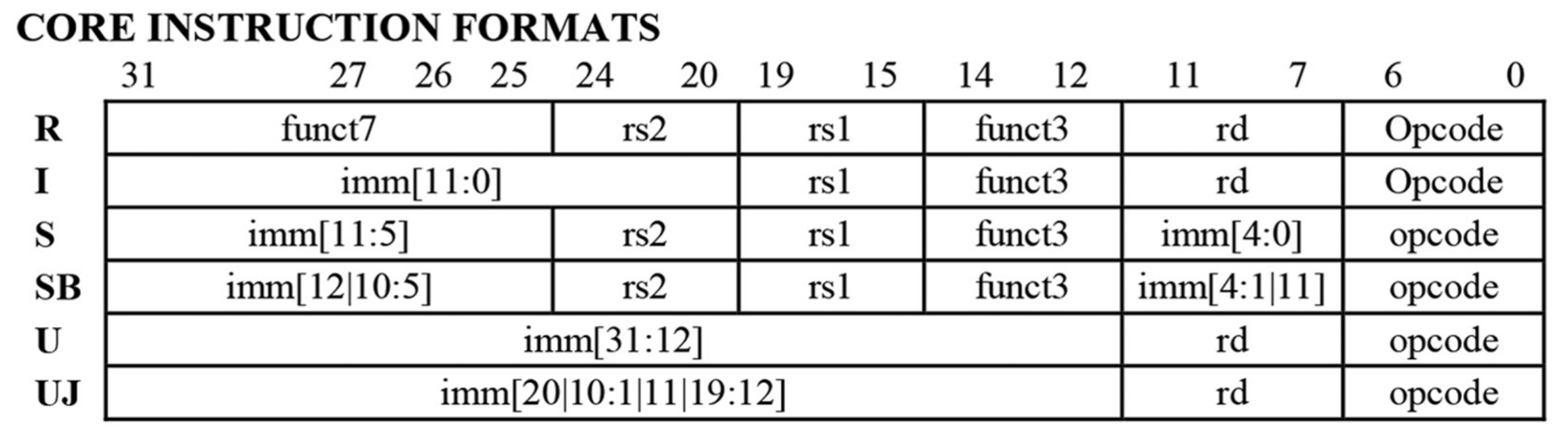
- format 和 instruction 的数量不需要这么多 bit 来区分:将来扩展?
- 为什么 R-format 要这么长的 func 来区分?
R-format
I-format
- load 和带 imm 的
- load 也是 I-f,类似 addi;有 LB,LBU,LH,LHU,LW,其中 U(unsigned) 是 zero-extend;正常是 sign-extend
S-format - store
SB-format - branch
- 重点是 imm 的分割,这样分看似复杂,优点在于相比于 S 的 imm,只改变了一位;其次方便 sign-extend
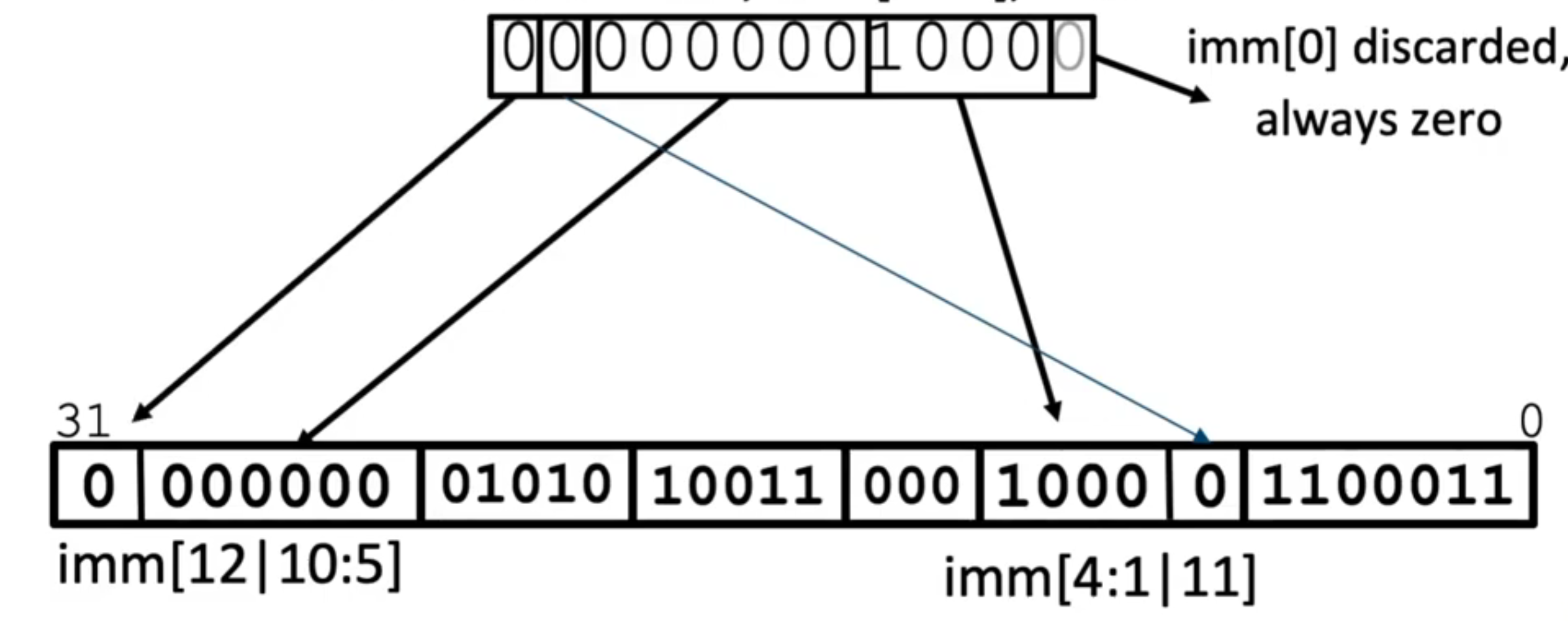
U-format- 存储 32bit imm
- 使用 lui, addi 组合可以创建 32bit imm,但是 addi 会 sign extend,导致 lui 前 20bit -1→需要手动给 lui +1(pesudo
li会隐式 +1)
UJ-format - 用来 jump(移动 pc)
- lui, jalr 组合可以指定绝对地址,auipc, jalr 组合可以指定 32bits offset
CALL
编译型语言从源代码到可执行文件的实际过程:Compiler, Assembler, Linker, Loader(CALL)
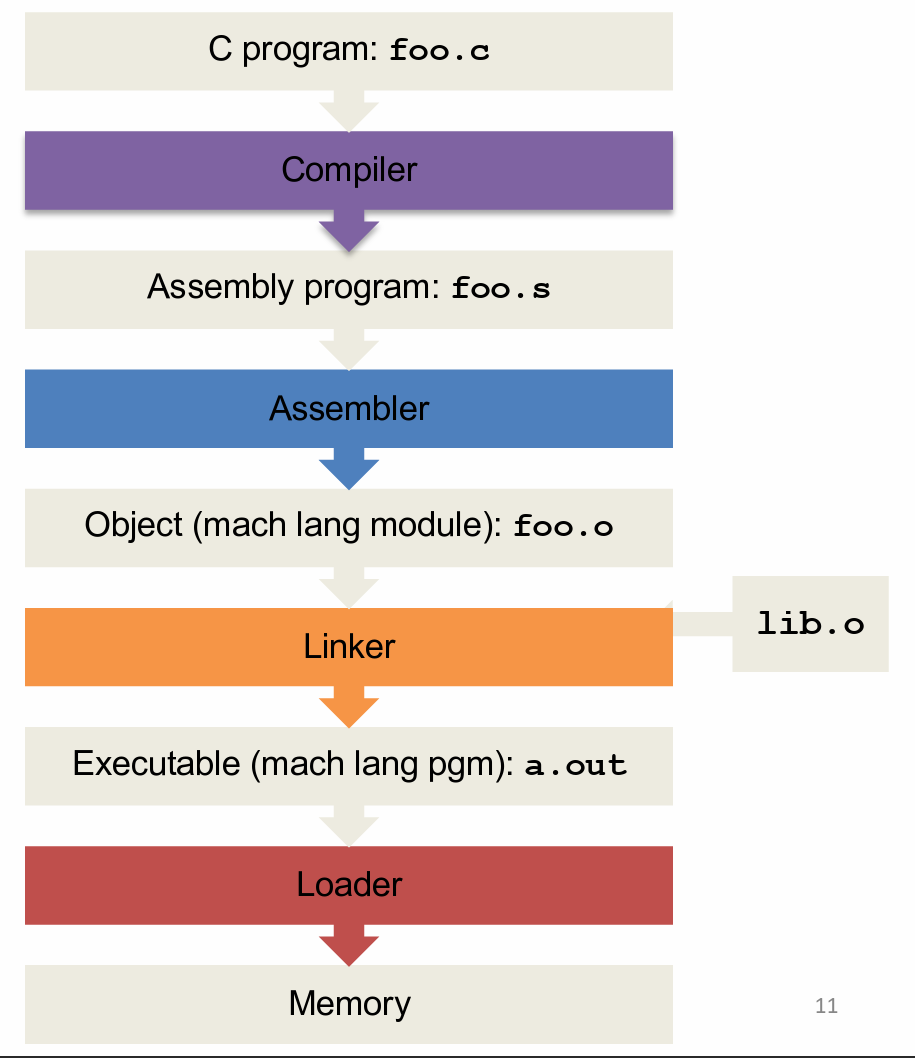
Compiler
High Level Language(HLL) → Assembly Language Code
Assembler
把汇编编程 object file(本质上是 assembly+infomation table)
这个阶段会过两遍代码
第一遍
- 替换伪指令
- 用 symbol table 记住 label 的位置
第二遍 - 使用 symbol table 产生相对(jump instruction 的)地址
- 把指令翻译成二进制
电路逻辑(Digital Logic)
Combinational Digital Logic(CL)
不记忆,输出只取决于输入
两种 channel,N,P
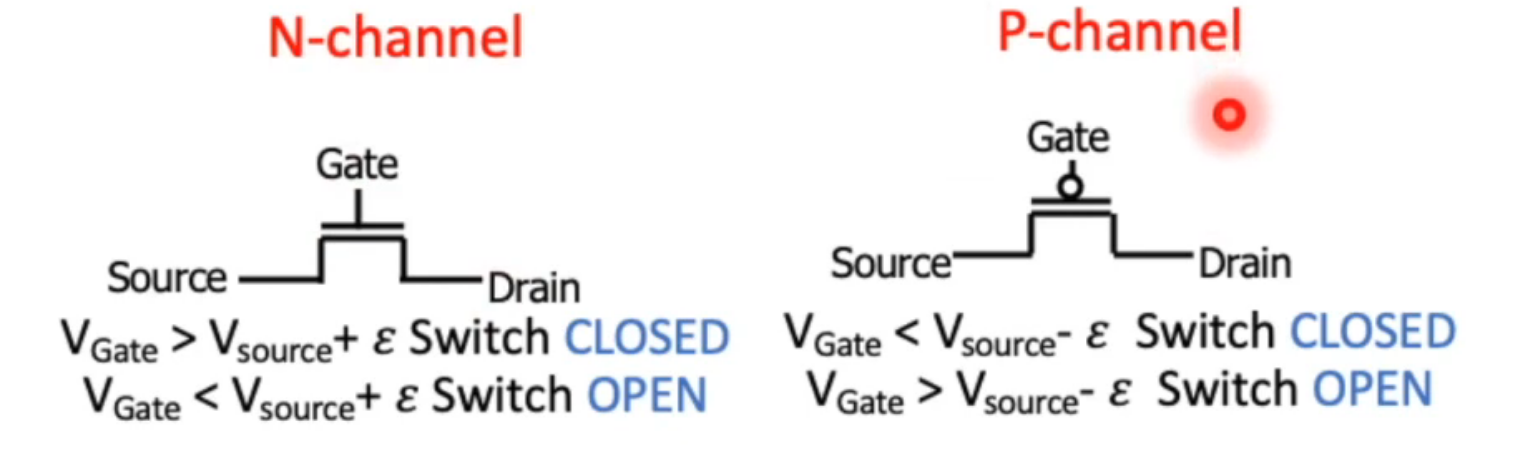
组合成 NOT, NAND, NOR gate,进而组合成各种逻辑门
布尔运算
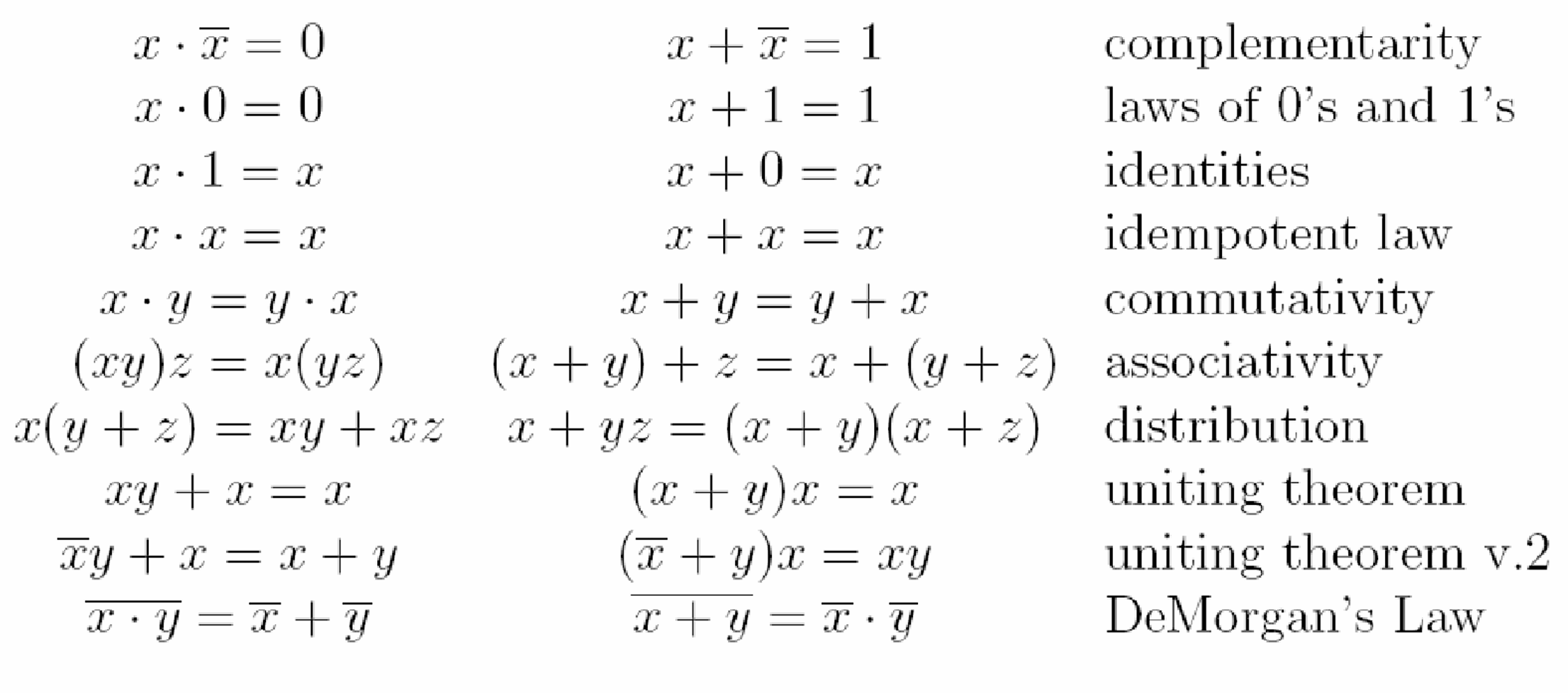
真值表,电路图和布尔表达式相互转化
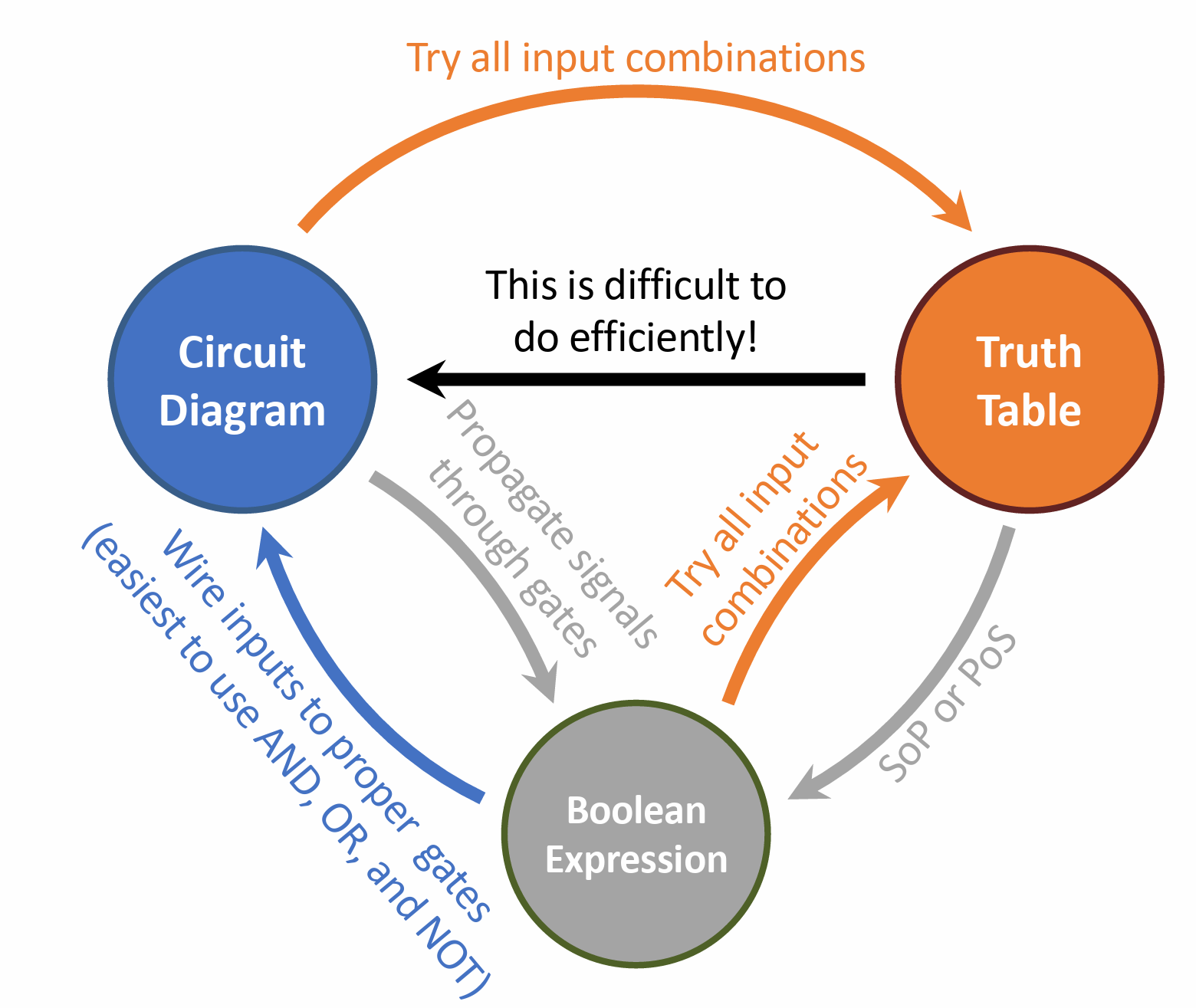
真值表描述输入输出,布尔表达式和电路描述逻辑关系
电路通过转化成布尔表达式来化简
Data Multiplexor(Mux)
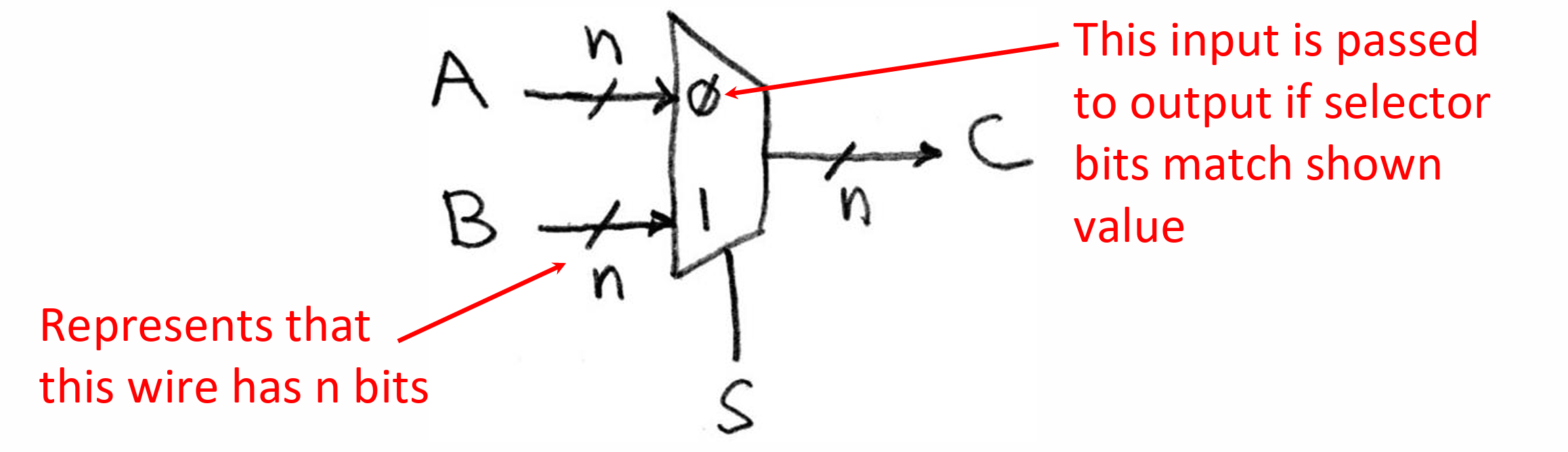
等价于
等价于
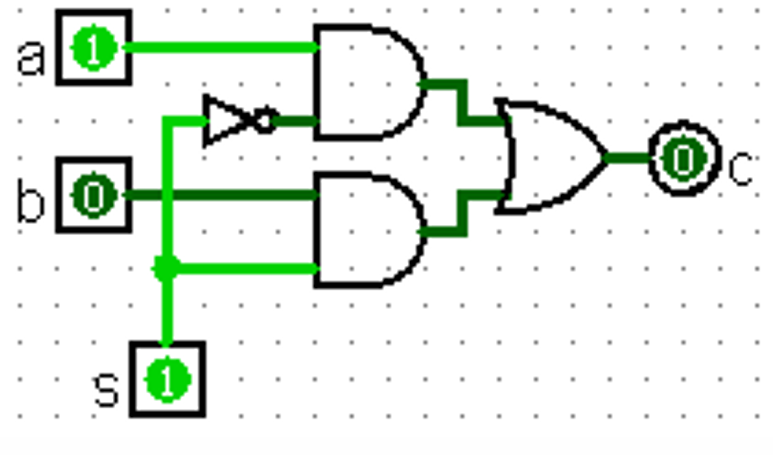
Sequential Digital Logic(SL)
会记忆信息,输出受记忆影响
e.g.: register
Register 原理
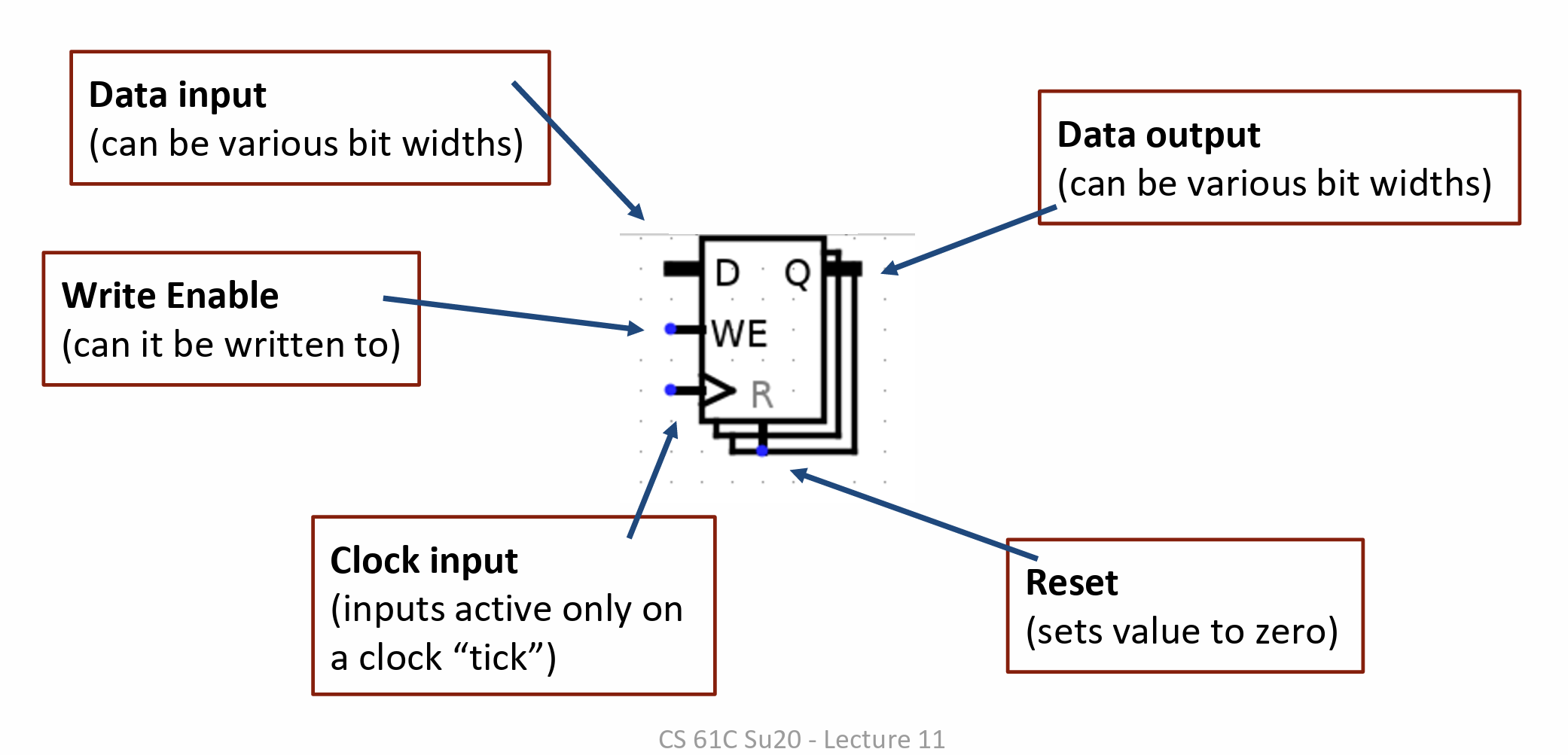
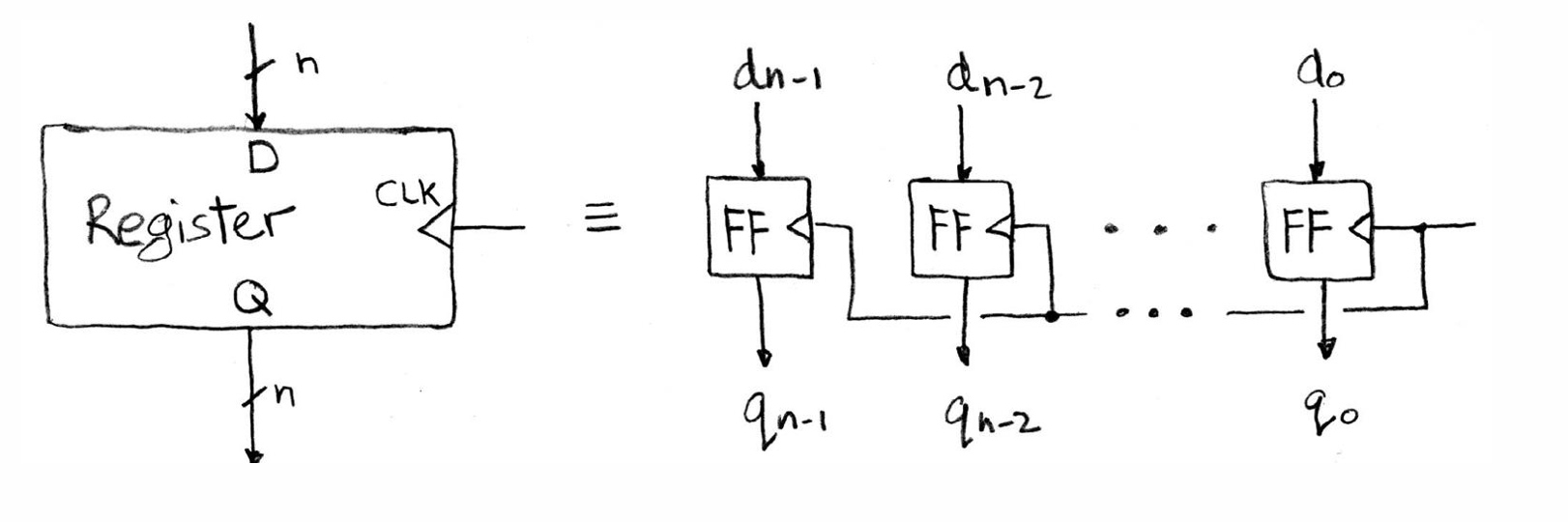
clock 电位周期变化
register 会在 clock 电位上升瞬间读取 D 的值,一段 delay 之后,把这个值写到 Q 上
几个阶段
- setup time: clock 触发前的一段时间,要求 D 的值稳定
- hold time: clock 触发后的一段时间,要求 D 的值稳定
- clock-to-Q: 从始终触发到 Q 被赋值的时间
accumulator 累加器

如果超频,会导致周期 T 时间缩短,导致 的垃圾值被 sample
频率最快能多快?
The critial path
在任意两个 register 之间的最长 delay
周期最短(频率最快)不能小于 critial path
pipeline 流水线
- 增加更多 register
- 可以减少每两个 register 之间的操作时间,让频率更快
- 但是会让总体时间增加,因为需要经过额外的 register
- 意味着对每个 input,花费更长时间,但是每秒可以有更多输出
Arithmetic Logic Unit(ALU)
- 使用 MUX 选择不同的运算
adder-subtractor
- N-bits 的加法分解成 1-bit 的加法
- 3 个输入:
两个输出:
判断溢出
- unsigned,
- signed,
减法
- 把相加的其中一个数取反,让 (由于二的补码)
相当于二进制的大数加法,此时可以用布尔运算算出每一位结果
Resources
- 课程地址 CS 61C 资源地址 CS 61C resources
- greensheet large green card